抄袭/参考资料
- 台湾大学《机器学习技法》视频
- 周志华《机器学习》
- 李航《统计学习方法》
- 决策树算法原理(下)
- 深入浅出ML之Tree-Based家族
分类与回归树(Classification And Regression Tree, 简称CART)模型在Tree家族中是应用最广泛的学习方法之一。它既可以用于分类也可以用于回归。
- 二叉树结构
- 分类树:基尼值
- 回归数:平方误差最小二乘
CART最大的特点就是只做二分,大大的减少了计算量,而且效果相当好,在实现了分类功能上,很轻松的转换到回归功能。
基尼值
在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益比来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢?有!CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。
具体的,在分类问题中,假设有$K$个类别,第$k$个类别的概率为$p_k$, 则基尼系数的表达式为:
$$
Gini(p) = \sum\limits_{k=1}^{K}p_k(1-p_k) = 1- \sum\limits_{k=1}^{K}p_k^2\\
二分类的情况:Gini(p) = 2p(1-p)
$$
对于个给定的样本$D$,假设有$K$个类别, 第$k$个类别的数量为$C_k$,则样本$D$的基尼系数表达式为:
$$
Gini(D) = 1-\sum\limits_{k=1}^{K}(\frac{|C_k|}{|D|})^2
$$
特别的,对于样本$D$,如果根据特征$A$的某个值$a$,把$D$分成$D_1$和$D_2$两部分,则在特征$A$的条件下,$D$的基尼系数表达式为:
$$
Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)
$$
大家可以比较下基尼系数表达式和熵模型的表达式,二次运算是不是比对数简单很多?尤其是二类分类的计算,更加简单。但是简单归简单,和熵模型的度量方式比,基尼系数对应的误差有多大呢?对于二类分类,基尼系数和熵之半的曲线如下:
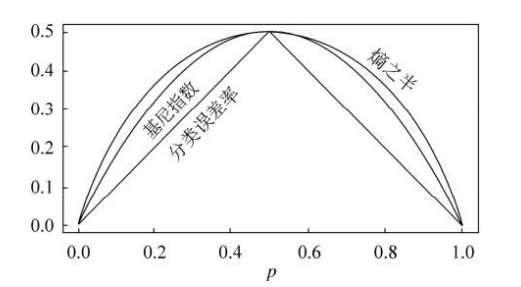
从上图可以看出,基尼系数和熵之半的曲线非常接近,仅仅在45度角附近误差稍大。因此,基尼系数可以做为熵模型的一个近似替代。而CART分类树算法就是使用的基尼系数来选择决策树的特征。同时,为了进一步简化,CART分类树算法每次仅仅对某个特征的值进行二分,而不是多分,这样CART分类树算法建立起来的是二叉树,而不是多叉树。这样一可以进一步简化基尼系数的计算$Gini(p) = 2p(1-p)$,二可以建立一个更加优雅的二叉树模型。
分类树只做二分的思路
相比ID3 和 C4.5的多叉树,CART只对特征做二分,需要对应的思路:
对离散值的二分处理
采用的思路是不停的二分离散特征。
举个例子,CART分类树会考虑把A分成${A1}和(A2,A3)$, ${A2}和(A1,A3)$, ${A3}和(1,A2)$ 三种情况,找到基尼系数最小的组合,比如${A2}和(1,A3)$然后建立二叉树节点,一个节点是$A2$对应的样本,另一个节点是$(A1,A3)$对应的节点。从描述可以看出,如果离散特征$A$有$n$个取值,则可能的组合有$n(n-1)/2$种。同时,由于这次没有把特征A的取值完全分开,后面我们还有机会在子节点继续选择到特征$A$来划分$A1$和$A3$.对连续特征的二分处理
思路同C4.5相近,划分$m-1$个点,之后采用不停的二分离散特征的做法,找到基尼值最小的点进行切分。
回归树
CART回归树和CART分类树的建立方式是一直的,只不过改动了下面两点
- 连续值的处理方法不同
对于连续值的处理,我们知道CART分类树采用的是用基尼系数的大小来度量特征的各个划分点的优劣情况。这比较适合分类模型,但是对于回归模型,我们使用了常见的均方差的度量方式,CART回归树的度量目标是,对于任意划分特征$A$,对应的任意划分点$s$两边划分成的数据集$D_1$和$D_2$,求出使$D_1$和$D_2$各自集合的均方差最小,同时$D_1$和$D_2$的均方差之和最小所对应的特征和特征值划分点。表达式为:
$$
\underbrace{min}_{A,s}\Bigg[\underbrace{min}_{c_1}\sum\limits_{x_i \in D_1(A,s)}(y_i - c_1)^2 + \underbrace{min}_{c_2}\sum\limits_{x_i \in D_2(A,s)}(y_i - c_2)^2\Bigg]
$$
- 决策树建立后做预测的方式不同。
对于决策树建立后做预测的方式,上面讲到了CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别,它采用的是用最终叶子的均值或者中位数来预测输出结果。