抄袭/参考资料

台湾大学《机器学习基石》视频
VC维的来龙去脉

Hoefiding不等式

$N$：样本量
$v$：样本均值
$u$：总体均值
$$
P\left [ v-u\geqslant \varepsilon \right ]\leqslant e^{-2\varepsilon ^{2}N}\\
P\left [ |v-u|\geqslant \varepsilon \right ]\leqslant 2e^{-2\varepsilon ^{2}N}
$$

学习的联系：单个假设

符号	描述说明
$H$	该机器学习方法的假设空间
$g$	表示我们求解的用来预测的假设($g$属于$H$)
$f$	理想的方案(可以是一个函数，也可以是一个分布)
$D$	样本集
$N$	样本量
$A$	算法

机器学习的过程就是：通过算法 $A$，在假设空间 $H$ 中，根据样本集 $D$，选择最好的假设作为 $g$ ，选择标准是 $g$ 近似于 $f$

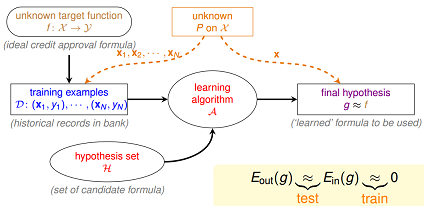
设定，$h(x)$是我们预估得到的某一个目标函数，$h(x)$是假设空间$H$中的一个假说。

${E_{out}}(h)$：(out-of-sample)总体损失期望
${E_{in}}(h)$：(in-of-sample)样本损失期望

基于hoeffding不等式，可得到下面公式，当样本量$N$足够大时，${E_{out}}(h)$和${E_{in}}(h)$将非常接近

$$
P\left [ |{E_{out}}(h)-{E_{in}}(h)|\geqslant \varepsilon \right ]\leqslant e^{-2\varepsilon ^{2}N}
$$

学习的联系：多个假设

注意在上面推导中，我们是针对某一个特定的解$h(x)$。在我们的假设空间$H$中，往往有很多个假设函数(甚至于无穷多个)

让我们先来理解下单个假设$h$的上限，其公式中的$2e^{-2\varepsilon ^{2}N}$（超出我们设定的 $\varepsilon$ 的样本集就是坏样本）就是这个假设h遇上坏样本的上限（上限只是最快的打算，大部分情况不会达到上限）

当多个假设存在，我们希望任意选择一个$h$都是每问题的，此时就需要标注出所有的坏数据集情况（对任意一个$h$是坏的，我就标注它是坏的）。那么我们任意选择一个$h$后 遇上坏样本的上限：就是所有$h$遇上坏样本的上限的并集。

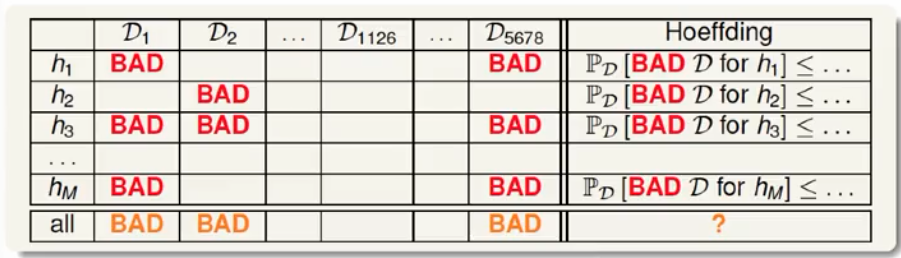
任意选择一个$h$后 遇上坏样本的上限如下图所示，但有个新问题，就是我们没法计算交集部分的大小（反正我不会）

注：灰色部分是每个$h$遇上坏样本的上限，而彩色部分是实际的概率

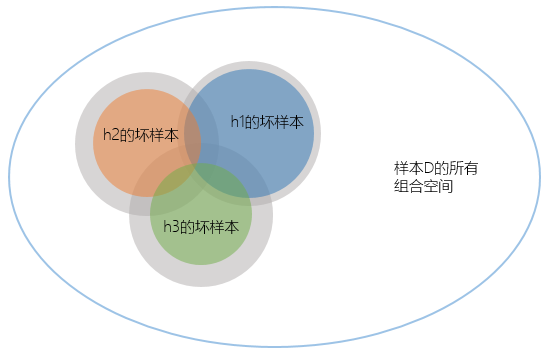
既然无法计算，但我们却知道每个单独的$h$遇上坏样本的上限：$2e^{-2\varepsilon ^{2}N}$，既然这样，我们只能计算其上限的上限了，交集就只剩简单的加法了

好，公式推导如下

我们根据样本集$D$，随机从假设空间$H$(假设有$M$个假设)中选取一个$h$，都会满足下面的公式

$$
P\left [ |{E_{out}}(h)-{E_{in}}(h)|\geqslant \varepsilon \right ]\leqslant Me^{-2\varepsilon ^{2}N}
$$

学习的可行性：两个核心条件

$$
P\left [ |{E_{out}}(h)-{E_{in}}(h)|\geqslant \varepsilon \right ]\leqslant Me^{-2\varepsilon ^{2}N}
$$

根据上一节得到的公式，我们得到学习可行的两个条件：

如果假设空间$H$的size $M$是有限的，当$N$足够大时，那么对假设空间中任意一个$g$，${E_{out}}(h)$约等于${E_{in}}(h)$.
利用算法$A$从假设空间$H$中，挑选出一个$g$，使得${E_{in}}(h)$接近于0，${E_{out}}(h)$也接近为0.

上面这两个核心条件，也正好对应着test和train这两个过程。train过程希望损失期望(即${E_{in}}(h)$ )尽可能小；test过程希望在真实环境中的损失期望也尽可能小，即${E_{in}}(h)$接近于${E_{out}}(h)$

Growth Function

证明了学习的可行后（满足两个核心条件），新问题又来了：$M$的大小！

	条件一	条件二
$M$太小	容易满足${E_{out}}(h)$约等于${E_{in}}(h)$	不容易找到一个${E_{in}}(h)$足够小的
$M$太大	不同意满足	选择多了，容易找到${E_{in}}(h)$足够小的

对于一个假设空间，$M$可能是无穷大的。要能够继续推导下去，那么有一个直观的思路，能否找到一个有限的因子 $m_H$ 来替代不等式bound中的$M$.

$$
P\left [ |{E_{out}}(h)-{E_{in}}(h)|\geqslant \varepsilon \right ]\leqslant 2 m_{H}e^{-2\varepsilon ^{2}N}
$$

在第三节中，我们把每个假设的代价都做了独立分离，但实际它们都是有重叠的部分，其中有一些甚至是完全重叠，我们可以把几乎重叠的假设归为一类，但把所有假设归类后，我们就能得到有效的假设数量Effective Number of Hypotheses——$m_H$

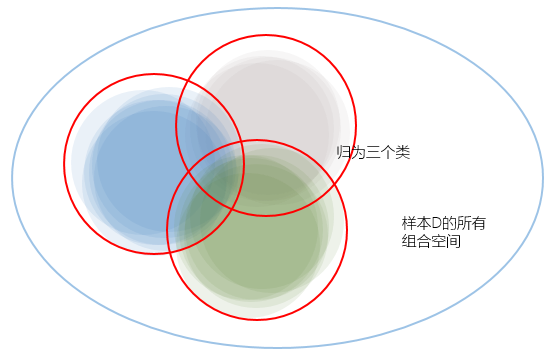
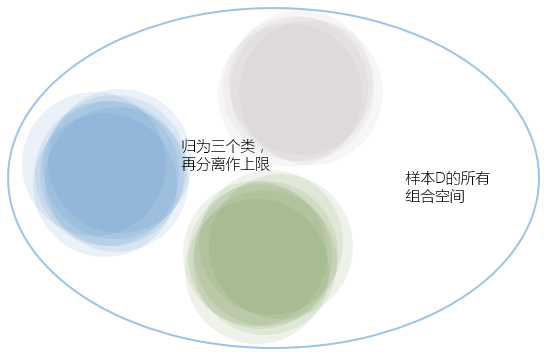
将所有假设进行分类的依据又是什么呢？答案就在样本集$D$，例如在$H$有两个假设（$M$中的两个，废话），它们作用于样本集后，得出的结果一致，我们就可以将它们两归为一类；反过来讲，根据样本集$D$我们能得出这一类的假设（$m_H$的一个）。

所以，$m_H$是一个比M小很多的数，而且它会是个根据样本集$D$数量$N$呈多项式增长的数，它的增长公式称为*成长公式Growth Function

$$
P\left [ |{E_{out}}(h)-{E_{in}}(h)|\geqslant \varepsilon \right ]\leqslant 2\cdot {effective}(N) e^{-2\varepsilon ^{2}N}
$$

~~成长公式的解释还没想好，就这样，next.~~

反正随着$N$增长，遇上坏样本的上限$2\cdot {effective}(N) e^{-2\varepsilon ^{2}N}$中一个是跟着多项式增长，一个跟着指数下降，指数必然打败多项式，所以总的来说随着$N$的增长，我们遇上坏样本的概率就会越来越低，${E_{out}}(h)$也就会越接近${E_{in}}(h)$. That’s good！

Break Point 和 Shatter

先切断一些，看看两个概念：shatter 和 break point.

Shatter的概念：当假设空间$H$作用于$N$个样本时，产生的dichotomies数量（二分类）等于这$N$个点总的组合数$2N$ 时，就称：这$N$个样本被$H$给shatter.掉了。
要注意到 shatter 的原意是“打碎”，在此指“$N$个点的所有(碎片般的)可能情形都被$H$产生了”。所以${m_H}(N)=2N$ 的情形是即为“shatter”。

Break Point的概念：对于给定的成长函数${m_H}(N)$，从$N=1$出发，$N$慢慢变大，当增大到$k$时，出现${m_H}(N)<2k$的情形，则我们说k是该成长函数的break poin.

当$N$的数量大于$k$时，$H$都没有办法再shatter他们了。

VC Bound

有了Break Point的概念后，如果break point存在（有限的正整数），对与任意的样本集，我们都可以得到成长函数的上界，经过推导可得：

$$
m_{H}(N)=\sum_{i=0}^{k-1}\binom{N}{i}
$$

多项式增长！多项式的最高幂次项为：$N^{k–1}$.
很开心，终于圆会Growth Function那一节的结论。

阶段性成果：能否用${m_H}(N)$直接替换M?

既然得到了m(N)的多项式上界，我们希望对之前的不等式中M 进行替换，用m_H(N)来替换M。这样替换后，当break point存在时，N足够大时，该上界是有限的。

然而直接替换是存在问题的，主要问题是：Ein的可能取值是有限个的，但$E_{out}$的可能取值是无限的。可以通过将$E_{out}$替换为验证集(verification set) 的$E_{in}$ 来解决这个问题。下面是推导过程：

VC Dimension

最后，VC维！暂时不想写，再理理！

计算学习原理

目录